Parábola

 La Parábola es una figura geométrica que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta (eje) y un punto fijo (foco) dados. 

La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas.

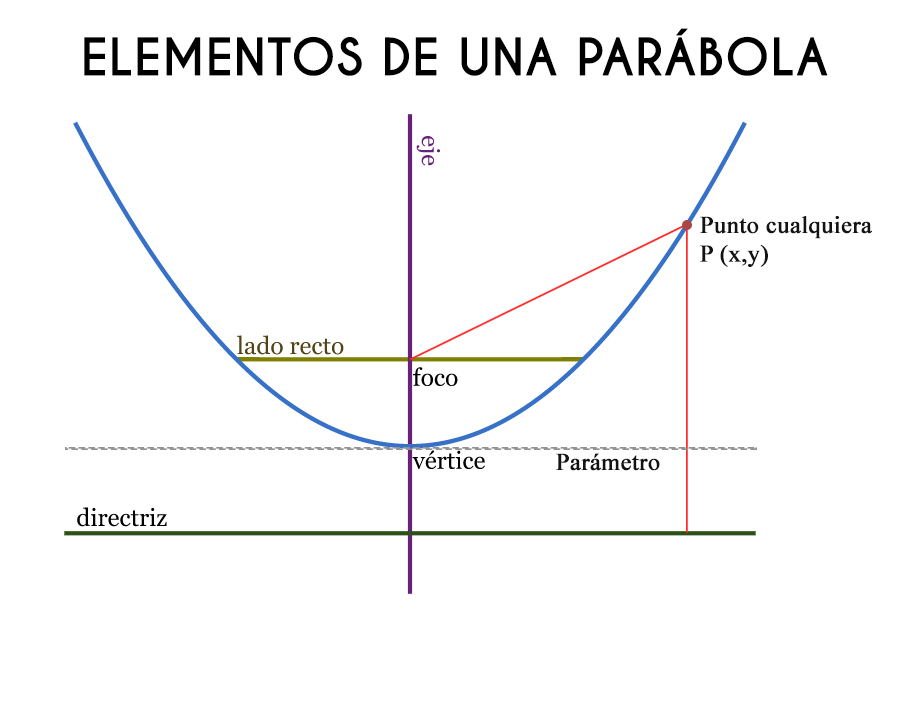
elementos de la parábola:

D: Directriz

V: Vértice

F: Foco

LR: Lado Recto

P: Significa parámetro es decir (la distancia del vértice al foco o a la directriz)



Parábola con vértice en el origen


-parábola horizontal


La ecuación canónica para una parábola horizontal es: 

 



Considerando que la parábola posee su vértice “V” justamente en el centro (0,0). Entonces sus elementos estarán distribuidos de la siguiente forma:

-  V(0,0)

-  Foco: F(p, 0)

- Ecuación de la Directriz: x = -p



Su concavidad:

Si p > 0 entonces decimos que la parábola abre hacia la derecha.

Si p < 0 entonces decimos que la parábola abre hacia la izquierda



-parábola vertical


La ecuación canónica para una parábola vertical es:  




Considerando que la parábola posee su vértice “V” justamente en el centro (0,0). Entonces sus elementos estarán distribuidos de la siguiente forma:

V(0,0)

Foco: F(0, p)

Ecuación de la Directriz: y = -p



Su concavidad:

Si p > 0 entonces decimos que la parábola es cóncava hacia arriba.

Si p < 0 entonces decimos que la parábola es cóncava hacia abajo.



Ejercicio:




Parábola con vértice fuera del origen


-parábola horizontal

Vemos que se trata de una parábola  horizontal, y que su vértice está  fuera del origen. Su eje es paralelo  al eje “X” y es cóncava hacia la  derecha o izquierda, según sea el  caso.



sus ecuaciones son:





Elementos de la parábola horizontal:








-parábola vertical


Vemos que se trata de una parábola  vertical, y que su vértice está fuera  del origen. Su eje es paralelo al eje  “Y” y es cóncava hacia arriba o  abajo, según sea el caso.


Sus ecuaciones son:





Elementos de la parábola vertical:

Se considera que la parábola posee su vértice “V” justamente en el punto  (h,k).








Ejercicio:

Determina la ecuación general de la parábola cuyo vértice y foco  son los puntos V(-5, 2) y F(-1, 2) 

respectivamente.




























Aplicaciones en la vida diaria:


-las parábolas se encuentran en nuestra vida cotidiana como los arcos en los puentes







- También en las antenas parabólicas que se caracterizan por llevar un reflector parabólico, cuya superficie es una paraboloide de revolución













Comentarios

Publicar un comentario

Entradas más populares de este blog

Ecuación de la recta que pasa por dos puntos dados

Imagen
  Por geometría la recta queda perfectamente determinada por dos cualesquiera de sus puntos; analíticamente, la ecuación de una recta también queda perfectamente determinada cuando se conocen las coordenadas de dos cualesquiera de sus puntos. La ecuación de la recta que pasa por dos puntos datos  Ejercicio: Hallar la ecuación de la recta que pasa por los puntos A (-3, -1) y B (5, 2) Aplicaciones en la vida diaria: -En las 10 primeras semanas de cultivo de una planta, que medía 2 cm al  comenzar, se ha observado que su crecimiento es directamente proporcional al  tiempo, viendo que en la primera semana ha pasado a medir 2.5 cm   -Una empresa que presta el servicio de gas tiene una cuota fija por servicio,  además cobra cierto valor por metro cubico consumido. Si por 25 m3 cobran $  22.000 y por 32 m3 $ 27.600, encontrar el valor del metro cubico consumido y la  cuota fija.
Leer más

Distancia entre dos puntos

Imagen
  Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas. distancia dirigida: Una distancia dirigida es una distancia que puede ser positiva o negativa. Por la convención, la distancia se toma generalmente para ser una cantidad positiva. En geometría analítica, una distancia dirigida puede ser utilizada. Esto es útil para medir la distancia de un punto del origen. Por la convención, una distancia dirigida positiva está al derecho, en vértice, o hacía del espectador.  Una distancia negativa está a la izquierda, abajo, o lejos del espectador. Un ejemplo de la distancia dirigida es una recta numérica con números negativos. Ejercicio: distancia no dirigida: Cuando hablamos de distancia no dirigida nos referimos a aquella distancia que existen entre 2 puntos, sin considerar la dirección de ellos. Por lo anterior utilizamos el valor absoluto de la dis...
Leer más