Circunferencia

A la circunferencia la podemos definir de la siguiente forma:

Es aquél lugar geométrico que describe un punto que se mueve en el plano de tal forma que su distancia a un punto fijo llamado centro, es siempre constante.

Dicha curva plana y cerrada la podemos encontrar de forma geométrica de la siguiente forma:






circunferencia con centro en el origen

Si el centro está en el origen de coordenadas del plano cartesiano, entonces una circunferencia de radio r se puede representar algebraicamente mediante la ecuación .


Ejercicio: 

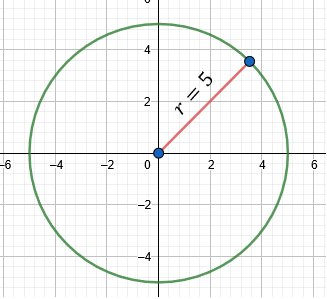
Determinar la ecuación de la circunferencia de centro en el origen cartesiano y de radio 5.



Resultado:

\displaystyle {{x}^{2}}+{{y}^{2}}=25

Ecuación de la Circunferencia


circunferencia con centro fuera del origen

en el caso de la ecuación fuera del origen, utilizaremos la forma ordinaria. Qué podemos apreciar en la siguiente fórmula:

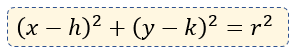
Ecuación de la Circunferencia fuera del origen

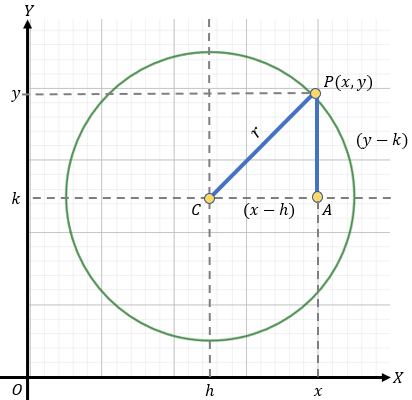
Circunferencia Fuera del Origen


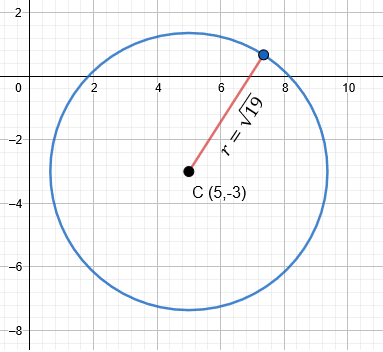
Ejercicio: Determinar la ecuación de la circunferencia cuyo centro es el punto C (5, -3) y su radio es de √19 

h = 5

k = -3

r = √19

ecuación ordinaria 

\displaystyle {{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}

\displaystyle {{(x-5)}^{2}}+{{(y-(-3))}^{2}}={{\left( \sqrt{19} \right)}^{2}}

Resultado:

\displaystyle {{(x-5)}^{2}}+{{(y+3)}^{2}}=19

Circunferencia fuera del origen



Aplicaciones en la vida diaria: 


-discos compactos:                                            

en la música se necesita precisión para que el disco tenga un correcto funcionamiento. Por lo tanto para la fabricación de estos se tienen que utilizar las técnicas del radio y diámetro




-transportes

un ejemplo son las ruedas de las bicicletas, las ruedas se afirman desde el centro y de ahi salen unos alambres delgados que se llaman "rayos" y esos alambres son el "radio" que mantienen la forma de circunferencia de la rueda sea perfectamente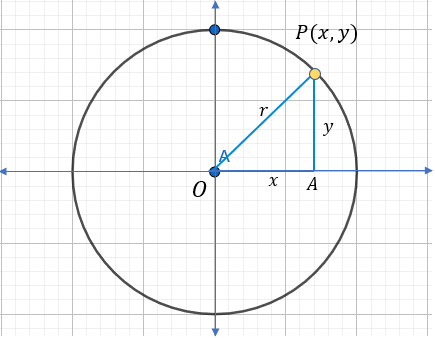



Comentarios

Publicar un comentario

Entradas más populares de este blog

Parábola

Imagen
  La  Parábola  es una figura  geométrica  que tiene forma de sección cónica, la cual resulta a partir de cortar en pequeños diferenciales un cono de punta redonda, se puede caracterizar también como el lugar geométrico de los puntos que equidistan de una recta  ( eje ) y un punto  fijo ( foco ) dados.  La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. elementos de la parábola: D:  Directriz V:  Vértice F:  Foco LR:  Lado Recto P:  Significa  parámetro  es decir (la distancia del vértice al foco o a la directriz) Parábola con vértice en el origen -parábola horizontal La ecuación canónica para una parábola horizontal es:    Considerando que la parábola posee su vértice “V” justamente en el centro (0,0) . Entonces sus elementos estarán distribuidos de la siguiente forma: -   V(0,0) -   Foco: F(p...
Leer más

Ecuación de la elipse con centro en el origen

Imagen
la elipse la podemos encontrar de manera horizontal y de manera vertical, con pequeños cambios en sus ecuaciones finales. elipse horizontal en una elipse horizontal el eje mayor coincide con el eje "x" Ecuación canónica: Elementos de la elipse en forma horizontal elipse vertical En   una    elipse    vertical el    eje  mayor  coincide con el eje “Y”. Ecuación canónica:  Elementos de la parábola vertical: Ejercicio: Determina  los  elementos y grafica la elipse,  cuya  ecuación es: 9x² + 4y² -36 = 0 Aplicaciones en la vida diaria: - Para  estudios científicos   como la trayectoria del átomo o sistemas solares. - Para la generación de piscinas,  tanques de agua , y recipientes para almacenar sustancias.
Leer más